作者个人研发的在高并发场景下,提供的简单、稳定、可扩展的延迟消息队列框架,具有精准的定时任务和延迟队列处理功能。自开源半年多以来,已成功为十几家中小型企业提供了精准定时调度方案,经受住了生产环境的考验。为使更多童鞋受益,现给出开源框架地址:
写在前面
应很多小伙伴的要求,我开了一个新的专题【程序员进阶系列】,在这个专题中,我会跟大家分享有关计算机和软件的一系列 底层 知识,让小伙伴们更好的理解计算机的底层架构知识,能够更好的提高自身的编程能力和软件设计能力。本篇就作为整个专题的开篇,希望能够为小伙伴们带来实质性的帮助。
数据的表示
在计算机中,所有的数据都是以二进制的形式进行表示的,也就是说,在计算机中使用0和1来表示所有的数据。而我们日常生活中的数字都是10进制的,那我们平时使用的数字如果在计算机中表示时就需要进行进制的转换。
进制转换
R进制转10进制
R进制转10进制可以使用按权展开的方法,具体的操作就是:将R进制数的每一位数值使用R^k^表示,底数是R,指数是k。其中,k与该位和小数点之间的位置有关。当这个位置位于小数据左边时,k的值是从小数点向左依次数的个数,需要注意的是:紧邻小数点的数字位置为0,接下来是1,2…依次类推。同样的,如果这个位置在小数点的右边,则紧邻小数据点位置的数字从-1开始,依次向右数为-2,-3等等,依此类推。
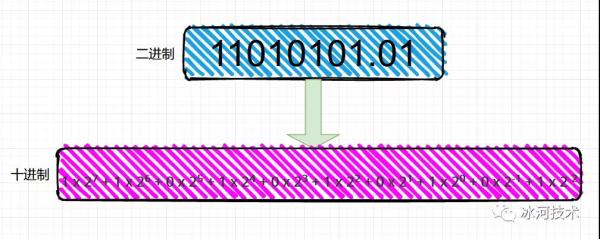
例如,我们给出一个二进制数字,11010101.01,转换为10进制数字为:1 x 2^7^ + 1 x 2^6^ + 0 x 2^5^ + 1 x 2^4^ + 0 x 2^3^ + 1 x 2^2^ + 0 x 2^1^ + 1 x 2^0^ + 0 x 2^-1^ + 1 x 2^-2^。
注:2^7^表示2的7次方。
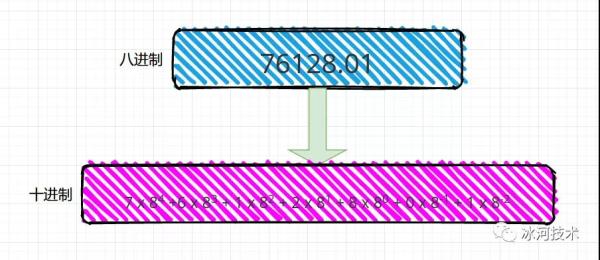
再比如,我们给出一个八进制数,76128.01,转换为10进制数字为:7 x 8^4^ +6 x 8^3^ + 1 x 8^2^ + 2 x 8^1^ + 8 x 8^0^ + 0 x 8^-1^ + 1 x 8^-2^
十进制转R进制
十进制转R进制就比较简单了,这里我们可以使用短除法。
例如,将十进制数字69转换为二进制的过程如下所示。
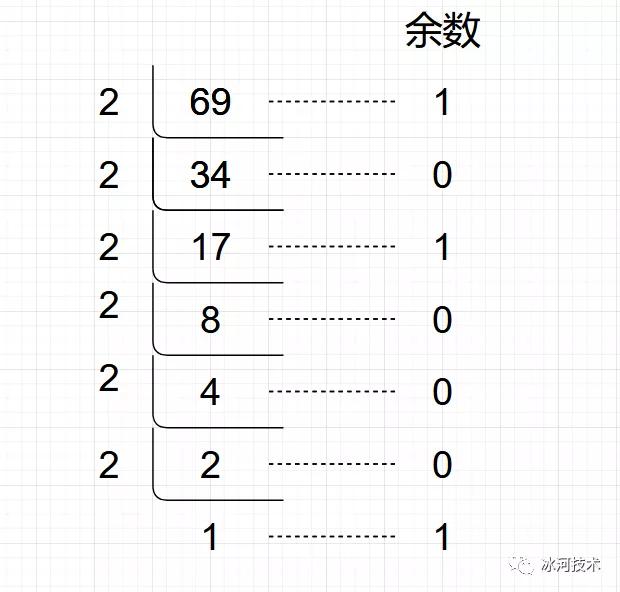
得出短除的结果后,我们需要将余数倒过来排列即为十进制69转换为二进制的结果,所以结果数据为:1000101。
二进制与八进制互转
二进制转八进制时,每三位二进制数表示一个八进制数。因为在八进制中,总共有8个基数,分别是0~7,逢8进1。而如果要使用二进制来表示时,0的二进制为000,7的二进制为111,所以,每三位二进制数对应一位八进制数。反过来,每一位八进制数对应三位二进制数。
具体的划分策略是,从二进制的低位开始,从低到高,也就是从右向左,每三位二进制数对应一个八进制数,不足三位的前面补0,例如,我们将二进制数:10001110转化为八进制数的过程,具体如下所示。
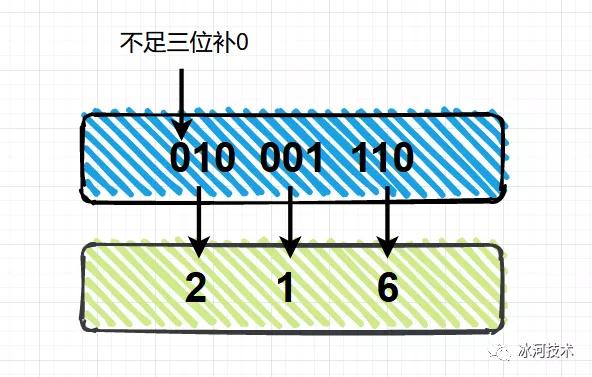
所以,二进制数10001110转化为八进制数的结果为216。
同理,八进制转二进制与二进制转八进制正好相反,八进制的每一位对应三位的二进制数。也就是说,将八进制数的每一位转化成三位的二进制数即可。
二进制与十六进制互转
在十六进制表示的数字中,总共有15个基数,为0~15,逢16进1。如果要将二进制数转化为十六进制数时,首先要弄清楚每位十六进制数需要多少为二进制数表示。在十六进制中,最大的基数为15,15的二进制表示为:1111,最小的基数为0,0的二进制数为0000,也就是说,十六进制的基础使用二进制表示为 0000~1111,所以,每位十六进制数需要四位二进制数表示。
从二进制数的低位开始,也就是从右侧开始,每四位二进制数对应一位十六进制数。
例如,我们需要将二进制数10001110转换为十六进制数,如下所示。
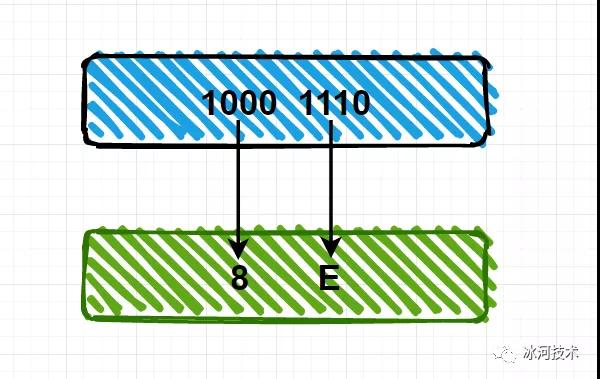
注意:在十六进制中,分别使用A,B,C,D,E,F代表10,11,12,13,14,15。
所以,二进制10001110转化为十六进制的结果为8E。
十六进制转二进制与二进制转十六进制正好相反,将十六进制的每一位转换为四位二进制数即可。
数据的码制
在计算机中,带符号的机器数可以采用原码、反码、补码和移码表示,这些编码称为码制。
原码
在原码表示中,最高位是符号位,0表示正号,1表示负号,其余的n-1位表示数值的绝对值,数值0的原码有两种表示形式:
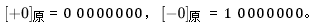
反码
在反码中,最高位是符号位,0表示正号,1表示负号,正数的反码与原码相同,负数的反码是其绝对值按位取反。数值0的反码有两种表示形式:
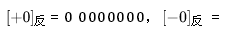
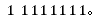
补码
在补码中,最高位是符号位,0表示正号,1表示负号,正数的补码与原码和反码相同,负数的补码等于其反码的末位加1。在补码的表示中,0有唯一的补码:
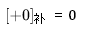
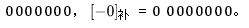
移码
移码表示法是在数X上增加一个偏移量来定义的,常用于表示浮点数中的阶码。如果机器字长为n,规定偏移量为 2^n-1^。
实际上,在偏移 2^n-1^的情况下,只要将补码的符号位取反就可以获得相应的移码。
码制总结
我们来看下面的表格,这里,我直接使用八位的二进制数来表示相应的数值。
码制 数值1 数值-1 1-1 原码 0000 0001 1000 0001 1000 0010 反码 0000 0001 1111 1110 1111 1111 补码 0000 0001 1111 1111 0000 0000 移码 1000 0001 0111 1111 1000 0000
通过表格我们发现:
正数的原码、反码和补码是相同的。 负数的反码是原码除符号位外,其他位分别取反; 负数的补码是其反码的末位加1。 移码是在补码的基础上符号位取反得到。
在负数的原码和补码的转换中,我们可以得出如下结论:
负数的原码转补码是在原码的基础上除符号位外,其他位取反,然后末位加1。 负数的补码转原码是在补码的基础上除符号位外,其他位取反,然后末位加1。
也就是说,负数的原码转补码和补码转原码的规则是一样的。小伙伴们可以根据表格自行验证
计算机使用补码进行加减法运算
我们再来看表格的最后一列 1-1,在计算机中,表示为1+(-1),其正确的结果应该为0。接下来,我们分别分析下使用原码、反码、补码和移码进行加减法运算的结果的正确性。
表格的第一行中,使用原码计算的结果为1000 0010,转换为10进制数为-2,1-1不等于-2,所以,使用原码进行加减法运算的结果是错误的。 在反码中,计算1-1的结果为1111 1111,显然结果不为0,所以,使用反码进行加减法运算的结果是错误的。 在补码中,计算1-1的结果为0000 0000,结果为0,所以,使用补码进行加减法运算的结果是正确的。 在移码中,计算1-1的结果为1000 0000,结果为-0,虽然-0也等于0,但是严格意义来讲,这个结果是不正确的。
在计算机中,不会使用移码进行加减法运算,移码用于浮点数的阶码。